Vectors and Kinematics – (Part 2 of 2)

You can find the first part of this series here: Vectors and Kinematics (Part 1 of 2).

Projectile Motion

Remember these acronyms: soh, cah, toa.

soh = sinº = opposite / hypotenuse

cah = cosº = adjacent / hypotenuse

toa = tanº = opposite / adjacent

• The opposite side is the one that is opposite the angle ‘x’

Example

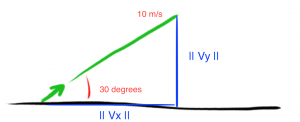
Consider a rocket is launched off at a 30º angle to the ground at 10 m/s.

Q. How far will it travel? (Horizontal displacement)

S denotes displacement

|| V_y || denotes magnitude of object in direction y

SOH, CAH, TOA

• sin(30) = || V_y || / 10 m/s
• 10 × sin(30) = || V_y ||
• 10 × ½ = || V_y ||
• 5 m/s = || V_y ||  ← This is the vertical component

However, the vertical component goes up, as well as down.

Initial = V_i = 5 m/s

Final = V_f = -5 m/s

• Δv_y = -5 m/s – 5m/s ⇒ -10 m/s
• Δv_y = a_y × Δt
• -10 m/s = -9.8 m/s² × Δt
• Divide both sides by -9.8 m/s²
• ∴ 1.02 seconds = Δt

For the horizontal component:

• Cos(30) = || Vx || / 10 m/s
• 10 × Cos(30) = || Vx ||
• || Vx || = 5√3 m/s

• S_x = 5√3 m/s × 1.02 seconds
• S_x = 8.83 meters

For the vertical component:

V_y = 5 m/s

Y axis meaning the up/down axis.

The positive value (+5 m/s) = the projectile is travelling up (y-axis); or to the right (x-axis). A negative value here would mean it was travelling downward (y-axis), or to the left (x-axis).

So, V_y = 5 m/s, meaning the object is travelling up @ 5 m/s

Q. How long does the rocket stay in the air?

• S = V_average × Δt
• S = (V_i + V_f)/2 × Δt

V_f = V_i + a × Δt

Deriving the formula:

• S = (V_i + V_i + a × Δt)/2 × Δt
• S = (V_i + a × Δt/2) × Δt
• S = V_i × Δt + (a +Δt²/2)

Now, at the start, S = 0

• 0 = 5 × Δt – (9.8(Δt²)/2)
• 0 = Δt × (5 – 4.9 × Δt)    ← one of these underlined, must equal 0
• If we assume  the first  Δt = 0, then:
• 5 = 4.9 × Δt
• 5/4.9 = (4.9 × Δt)/4.9
• Δt = 1.02 seconds

Recommended Reading for Physics